 Se entiende por rigor matemático (o también, «precisión matemática», aunque en un contexto algo diferente) una manera lógica y clara de trabajar dentro del ámbito de las matemáticas. Engloba, por una parte, aquel proceder axiomático a partir de definiciones y, por otra, la obligatoriedad de la demostración, un sistema de pasos que usa necesariamente la hipótesis y otros pasos justificados con proposiciones previas dentro de la teoría respectiva. Además, se pretende seguir el método de la deducción sistemática. Como consecuencia de la aplicación del rigor matemático, los teoremas son por principio verdades definitivas y de vigencia general, de modo tal que la matemática puede ser considerada la ciencia exacta. El rigor matemático no constituye un fin en sí mismo, sino un medio necesario para posibilitar progresos perdurables en la matemática. El rigor es también, en el sentido griego, una buena "escuela de pensamiento". Como efecto ulterior, el rigor matemático también arroja por resultado una simplificación de las explicaciones y demostraciones matemáticas.
Se entiende por rigor matemático (o también, «precisión matemática», aunque en un contexto algo diferente) una manera lógica y clara de trabajar dentro del ámbito de las matemáticas. Engloba, por una parte, aquel proceder axiomático a partir de definiciones y, por otra, la obligatoriedad de la demostración, un sistema de pasos que usa necesariamente la hipótesis y otros pasos justificados con proposiciones previas dentro de la teoría respectiva. Además, se pretende seguir el método de la deducción sistemática. Como consecuencia de la aplicación del rigor matemático, los teoremas son por principio verdades definitivas y de vigencia general, de modo tal que la matemática puede ser considerada la ciencia exacta. El rigor matemático no constituye un fin en sí mismo, sino un medio necesario para posibilitar progresos perdurables en la matemática. El rigor es también, en el sentido griego, una buena "escuela de pensamiento". Como efecto ulterior, el rigor matemático también arroja por resultado una simplificación de las explicaciones y demostraciones matemáticas.

Cauchy fue un profesor impopular tanto entre los estudiantes como entre sus compañeros de facultad. Sus clases eran muy densas y difíciles de seguir, muchas veces prolongaba la clase más allá de su horario oficial y además realizaba continuas revisiones del temario. Para Cauchy las matemáticas del siglo XVIII eran una disciplina que había perdido el norte. Todo un siglo de innovaciones matemáticas maravillosas que habían sido logradas a costa del rigor. Matemáticos como Euler manejaban series que no eran convergentes y expresiones formales sin sentido que producían conclusiones absurdas. No estaban claros conceptos tan básicos como el de infinito, el de límite, los números imaginarios y muchos más. Cauchy admiraba la formulación axiomática de la geometría realizada por Euclides. El álgebra presentaba un estado similar, pero era considerada por los matemáticos del siglo XVIII como una herramienta, versátil, pero de poca utilidad a la hora de resolver problemas prácticos. Por el contrario, el análisis era muy útil en todo tipo de problemas prácticos, pero carecía de un formulación rigurosa. Cauchy quería que el status de la geometría y del álgebra fuera extendido al análisis. Por ello decidió revisar todo el análisis desde el punto de vista de la geometría y apoyado por el álgebra como herramienta.
Por supuesto, el “Curso de Análisis” de Cauchy, como suele ocurrir con todo trabajo pionero, carece de rigor en muchos aspectos. Por ejemplo, Cauchy asume que todas las funciones continuas son diferenciables. Sin embargo, lo importante del proyecto de reforma del análisis iniciado por Cauchy, que trata de llevar el rigor al análisis de la mano de la geometría y del álgebra, es que inició un camino hacia el rigor cuya culminación fue el motor de gran parte de la matemática de todo el siglo XIX, con la honrosa excepción del genial Henri Poincaré que vio en el rigor un corsé del que había que deshacerse.
El cénit del rigor en las matemáticas llegó en el siglo XX con Nicolas Bourbaki, el nombre colectivo de un grupo de matemáticos franceses que, en los años 1930, se pusieron a revisar todos los fundamentos de las matemáticas con una exigencia absoluta en el rigor tratando de combatir la corriente que había nacido con Poincaré. Matemáticos como Jean Dieudonné, André Weil, Henri Cartan, Claude Chevalley, y otros antiguos alumnos de la Escuela Normal Superior de París recogieron el guante de Cauchy e impusieron a toda la matemática el concepto de rigor matemático como definición de la labor del matemático.
Un matemático es una máquina de demostrar teoremas con absoluto rigor. La máxima revolucionaria de Bourbaki es Vive la rigueur!
Recuperado de:http://francis.naukas.com/2013/10/27/cauchy-y-el-rigor-en-el-analisis-matematico/ y https://es.wikipedia.org/wiki/Rigor_matem%C3%A1tico








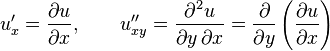
 para las
para las  ) para las derivadas que involucran el tiempo, por ejemplo para escribir la
) para las derivadas que involucran el tiempo, por ejemplo para escribir la 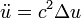 (notación matemática)
(notación matemática) (notación física)
(notación física)