 de varias variables independientes
de varias variables independientes  y las derivadas parciales de
y las derivadas parciales de  respecto de esas variables. Las ecuaciones en derivadas parciales se emplean en la formulación matemática de procesos de la física y otras ciencias que suelen estar distribuidos en el espacio y el tiempo. Problemas típicos son la propagación del sonido o del calor, la electrostática, la electrodinámica, la dinámica de fluidos, la elasticidad, la mecánica cuántica y muchos otros. Se las conoce también comoecuaciones diferenciales parciales. Participaron, al inicio, en su estudio los franceses D'alambert, Fourier, matemáticos de la época napoleónica.
respecto de esas variables. Las ecuaciones en derivadas parciales se emplean en la formulación matemática de procesos de la física y otras ciencias que suelen estar distribuidos en el espacio y el tiempo. Problemas típicos son la propagación del sonido o del calor, la electrostática, la electrodinámica, la dinámica de fluidos, la elasticidad, la mecánica cuántica y muchos otros. Se las conoce también comoecuaciones diferenciales parciales. Participaron, al inicio, en su estudio los franceses D'alambert, Fourier, matemáticos de la época napoleónica.Notación y ejemplos
En las ecuaciones diferenciales en derivadas parciales es muy común denotar las derivadas parciales empleando sub-índices (Notación tensorial). Esto es:
Especialmente en la física matemática, se suele preferir el operador nabla (que en coordenadas cartesianas se escribe como  para las derivadas espaciales y un punto (
para las derivadas espaciales y un punto ( ) para las derivadas que involucran el tiempo, por ejemplo para escribir la Ecuación de onda (véase más abajo) como
) para las derivadas que involucran el tiempo, por ejemplo para escribir la Ecuación de onda (véase más abajo) como
 para las derivadas espaciales y un punto (
para las derivadas espaciales y un punto ( ) para las derivadas que involucran el tiempo, por ejemplo para escribir la Ecuación de onda (véase más abajo) como
) para las derivadas que involucran el tiempo, por ejemplo para escribir la Ecuación de onda (véase más abajo) como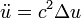 (notación matemática)
(notación matemática)
 (notación física)
(notación física)
Recuperado de: https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_en_derivadas_parciales
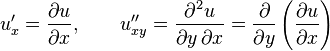
No hay comentarios.:
Publicar un comentario